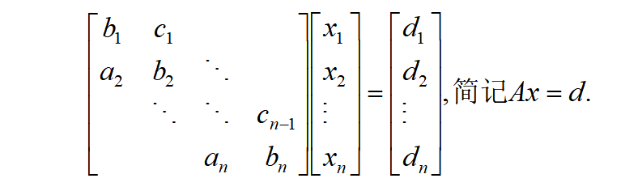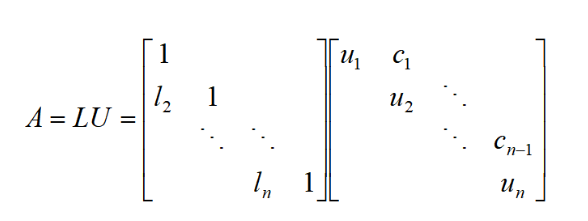前言

不知道为什么忽然想快速学一下这门课，所以就快速学一下这门课了。

书籍参考《数值分析》何汉林、梅家斌主编和《实用数值分析》杜迎春主编的两本书，因为我目前就找到了这两本书，图书馆借的，马上就要到期了。

第一章 绪论

第1节 什么是数值分析

数值分析也称计算方法，是数学科学的一个重要分支，它是研究计算机求解数值解的计算方法及其软件实现。

第2节 数值计算的误差

• 第一类是截断误差或方法误差：将数学问题转化为计算问题时产生的误差，比如泰勒近似会引入一个小误差。
• 第二类是舍入误差：在计算中由于保留小数位有限而造成的误差。

设准确值x的近似值为x*，则$e(x*)=x-x*$称为x*的绝对误差，绝对误差一般无法求解精确值，只能得出误差限$\delta(x*)$。$e_r(x*)=\frac{x-x*}{x}$被称为相对误差。

第二章 直接法解线性方程组

$$\left\{ \begin{array}{} a_{11}x_1 + a{12}x_2 + \dots + a_{1n}x_n = a_{1,n+1} \\ a_{21}x_1 + a{22}x_2 + \dots + a_{2n}x_n = a_{2,n+1} \\ \dots\quad \dots\\ a_{n1}x_1 + a{n2}x_2 + \dots + a_{nn}x_n = a_{n,n+1} \end{array} \right.$$

第1节 消元法

• Gauss消元法：毫无疑问，在线性代数中肯定学过，如果没有学过线性代数的话，可以先去学线性代数。也就是将矩阵先化成上三角矩阵，然后再自下而上的求解。
• Gauss-Jordan消去法：与高斯消元法类似，不过是先化成对角矩阵，然后再求解。

无论是哪种消元法，其计算的复杂度都是$O(n^3)$级别的。

除此之外，还有主消元法。主消元法是由于直接消元法在计算中可能会导致较大的误差，所以需要用主消元法。主元是指：绝对值最大的元素。

第2节 直接三角分解法

• A=LU分解：L是下三角矩阵，U是上三角矩阵，A需要是非奇异方阵且1至n-1阶的顺序主子式不等于0。
• A=LDU分解：L是下单位三角矩阵，D是对角矩阵，U是上单位三角矩阵。A需要是非奇异方阵，且充要条件是各阶顺序主子式不为0.（单位三角矩阵是指对角线全1）
• A=PLU分解：P是置换矩阵，L是下三角矩阵，U是上三角矩阵。

第3节追赶法

追赶法适用于快速求解三对角矩阵方程，如下图所示：

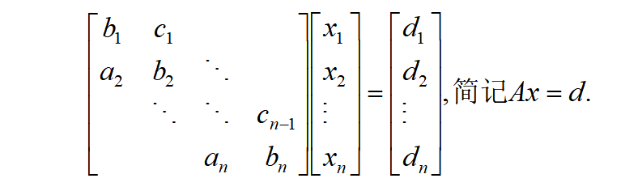
求解步骤：

1. 分解成A=LU（并且其中蕴含着A=Ly，y=Ux）

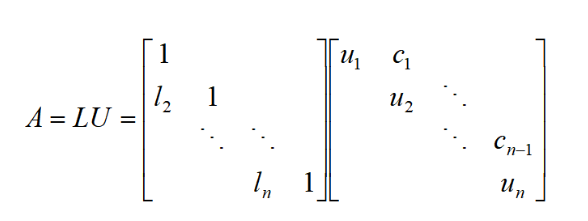
2. 给出分解公式：

$$l_i = \frac{a_i}{u_{i-1}} \quad 2\leq i\leq n \\u_i = \left\{ \begin{array}{} b_1,& i=1\\ b_i-c_{i-1}l_i,& 1<i\leq n \end{array} \right.$$

3. 解Ly=d:

$$y_i = \left\{ \begin{array}{} d_1, &i=1\\ d_i - l_iy_{i-1},& 1<i\leq n \end{array} \right.$$

4. 解Ux=y：

$$x_i = \left\{ \begin{array}{} \frac{y_n}{u_n}, & i=n\\ \frac{y_i-c_ix_{i+1}}{u_i},& n>i\geq 1 \end{array} \right.$$

第4节 范数

• 向量范数：也就是向量的模，记为$\|x\|$。在向量空间$R^n$中最常见的向量范数有以下3种：

  1. 无穷范数：$\|x\|_\infty = \max(|x_1|, |x_2|,\dots,|x_n|)$
  2. 1-范数：$\|x\|_1 = |x_1|+|x_2|+\dots+|x_n|$
  3. 2-范数：$\|x\|_2 = \sqrt{x_1^2+x_2^2+\dots+x_n^2}$

• 矩阵范数：$\|A\| = \max\limits_{x\neq0}\frac{\|Ax\|}{\|x\|}=\max\limits_{\|x\|=1}\|Ax\|$。

  $\|A+B\|\leq \|A\|+\|B\|$

  $\|Ax\|\leq\|A\|\|x\|$

  $\|AB\|\leq\|A\|\|B\|$

  同理，矩阵范数仍然有三种，设A为n阶方阵

  1. $\|A\|_\infty = \max\limits_{1\leq i\leq n}\sum\limits_{j=1}^n|a_{ij}|$
  2. $\|A\|_1 = \max\limits_{1\leq j\leq n}\sum\limits_{i=1}^n|a_{ij}|$
  3. $\|A\|_2 = \sqrt{方阵A^TA的最大特征值}$

• 条件数：设A是非奇异方阵，条件数记为$cond(A)=\|A^{-1}\|\cdot\|A\|$

  1. $cond_1(A) = \|A\|_1 \cdot \|A^{-1}\|_1$
  2. $cond_\infty (A) = \|A\|_\infty\cdot\|A^{-1}\|_\infty$
  3. 谱条件数：$cond_2(A) =\|A\|_2\cdot\|A^{-1}\|_2 = \sqrt{\frac{\lambda_{max(A^TA)}}{\lambda_{min(A^TA)}}}=\frac{|\lambda_{max(A)}|}{|\lambda_{min(A)}|}(A是对称矩阵)$，$\lambda$是特征值。

第三章 迭代法解线性方程组

第1节 Jacobi迭代法

$$\left\{ \begin{array}{} a_{11}x_1 + a{12}x_2 + \dots + a_{1n}x_n = b_1 \\ a_{21}x_1 + a{22}x_2 + \dots + a_{2n}x_n = b_2 \\ \dots\quad \dots\\ a_{n1}x_1 + a{n2}x_2 + \dots + a_{nn}x_n = b_n \end{array} \right.$$

可以把上式记为Ax=b。把A分解成D和R的和，即A=D+R。

$$A = \begin{bmatrix} a_{11} & a_{12} & \dots & a_{1n}\\ a_{21} & a_{22} & \dots & a_{2n}\\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \dots & a_{nn} \end{bmatrix} = D+R$$

其中，D和R分别为：

$$D = \begin{bmatrix} a_{11} & 0 & \dots & 0\\ 0 & a_{22} & \dots & 0\\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dots & a_{nn} \end{bmatrix},\quad R =\begin{bmatrix} 0 & a_{12} & \dots & a_{1n}\\ a_{21} & 0 & \dots & a_{2n}\\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \dots & 0 \end{bmatrix}$$

带入Ax=b，并令左边的x为新的迭代值，右边的x为旧的迭代值。

$$Dx = b-Rx \quad\Rightarrow\quad x^{(k+1)} = D^{-1}(b-Rx^{(x)})$$

代入得到迭代通式：

$$x^{(m+1)}_i \\= \frac{1}{a_{ii}}\left( b_i - \sum\limits_{j=1}^{i-1}a_{ij}x^{(m)}_j- \sum\limits_{j=i+1}^{n}a_{ij}x^{(m)}_j\right) \\= \frac{1}{a_{ii}}\left( b_i - \sum\limits_{j=1}^{n且j\neq i}a_{ij}x^{(m)}_j\right)(i = 1,2,\dots,n;m=0,1,2,\dots) \\$$

其中m是迭代次数。对于初值，也就是$x^{(0)}$，需要设定一个初值。

第2节 Seidel迭代法

与前面的Jacobi迭代法通式只有一点不同，同样求解Ax=b，把A分解成A=L+D+U

$$L = \begin{bmatrix} 0 & 0 & \dots & 0\\ a_{21} & 0 & \dots & 0\\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \dots & 0 \end{bmatrix},\quad D = \begin{bmatrix} a_{11} & 0 & \dots & 0\\ 0 & a_{22} & \dots & 0\\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dots & a_{nn} \end{bmatrix},\quad U = \begin{bmatrix} 0 & a_{12} & \dots & a_{1n}\\ 0 & 0 & \dots & a_{2n}\\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dots & 0 \end{bmatrix}$$

然后带入Ax=b，并且令L的x和D的x为新的迭代值，令U的x为旧的迭代值

$$Dx=b-Lx-Ux\quad\Rightarrow\quad \\ Dx^{(k+1)} = b-Lx^{(k+1)}-Ux^{(k)}\quad\Rightarrow\quad \\ x^{(k+1)} = (D+L)^{-1}(b-Ux^{(m)})$$

代入得到迭代通式：

$$x^{(m+1)}_i \\= \frac{1}{a_{ii}}\left( b_i - \sum\limits_{j=1}^{i-1}a_{ij}x^{(m+1)}_j- \sum\limits_{j=i+1}^{n}a_{ij}x^{(m)}_j\right)$$

注意第一个求和只是[1, i-1]求和，然后假设我们需要求第i个$x^{(m+1)}_i$的值时候，我们已经把所有小于i（j<i）的$x_j^{(m+1)}$求解出来了，所以这里逻辑是说得通的。通过这里我们发现，跟Jacobi最大的区别是，这里求新的迭代值时候，只能串行求解，不能并行求解。

第3节 SOR方法

 超松弛迭代法（successive over relaxation method）是对Seidel迭代法的一种加速方法，是解其系数矩阵为大型稀疏矩阵的方程组的一种有效方法。

$$\hat{x}^{(m+1)}_i \\= \frac{1}{a_{ii}}\left( b_i - \sum\limits_{j=1}^{i-1}a_{ij}x^{(m+1)}_j- \sum\limits_{j=i+1}^{n}a_{ij}x^{(m)}_j\right)$$

这里的$\hat{x}_i$就是跟Seidel中的$x_i$一样的，但是这里是引入的一个中间变量。另外，再引入一个松弛参数$\omega$，真正的$x_i$应该是：

$$x_i^{(m+1)} = (1-\omega)x_i^{(m)}+\omega \hat{x}^{(m+1)}_i \\ = x_i^{(m)} + \frac{\omega}{a_{ii}}(b_i - \sum\limits_{j=1}^{i-1}a_{ij}x_j^{(m+1)}-\sum\limits_{j=i}^na_{ij}x_j^{(m)})$$

如果$\omega>1$则称为超松弛迭代法；如果$\omega<1$则称为低松弛迭代法；当$\omega=1$时，就是Seidel迭代法。

下面给出一些定理：

• Ax=b的系数矩阵为实对称正定且$0<\omega<2$时，SOR法收敛。
• 如果A是三角对称正定矩阵，$B_1,B_2$分别为Jacobi和Seidel迭代矩阵，则有：
  • $\rho(B_2)=(\rho(B_1))^2 < 1$
  • 最佳松弛因子：$\omega_{o\rho}=\frac{2}{1+\sqrt{1-\rho(B_2)}}$
  • 松弛迭代矩阵 $B_\omega$ 的谱半径：$\rho(B_\omega)=\omega-1$，其中谱半径是指矩阵特征值的绝对值最大值，$\max\{|\lambda_1|, |\lambda_2|,\dots,|\lambda_n|\}$

第三章 非线性方程求根

非线性方程有两类，一类是含有三角函数、对数函数、指数函数及其他超越函数的方程，称为超越方程；另一类重要的方程是：

$$f(x)=a_0+a_1x+a_2x^2+\dots+a_nx^n=0\quad(a_n\neq0)$$

第1节 搜索法

假设给定区间[a,b]，f(x)再这个区间上连续且满足：f(a)f(b)<0

• 直接搜索：也就是从起点a开始，给定步长依次往终点b搜索。找到连续两个点$x_i,x_{i+1}$，但是其符号不同，所以最终结果为$\frac{x_i+x_{i+1}}{2}$
• 二分法搜索：取中点 c，如果f© = 0，c就是根；如果f(a)f©<0，则根在[a,c]中；如果f(a)f©>0，则根在[c,b]中；继续步骤

第2节 迭代法

只需要把$f(x)=0$改写成$x=\phi(x)$的形式，然后迭代函数：$x_{k+1}=\phi(x_k)$，现在需要考虑一下这种迭代是否收敛。

• 压缩印象定理：若函数$\phi(x)$在区间[a,b]上具有一阶连续的导数，且满足：

  1. 封闭性，即当$x\in [a,b]$时，$\phi(x)\in[a,b]$
  2. 压缩性，存在正常数L<1(L称为压缩系数)，使得对任意$x\in[a,b]$有$|\phi'(x)|\leq L$，则

  1. 方程$x=\phi(x)$在[a,b]上有唯一实根$x^*$
  2. 对任意$x_0 \in [a,b]$，$\lim\limits_{k\rightarrow \infty}x_k = x^*$
  3. 误差事后估计式：$|x_k-x^*|\leq \frac{L}{1-L}|x_k-x_{k-1}|$
  4. 误差事前估计式：$|x_k-x^*|\leq\frac{L^k}{1-L}|x_1-x_0|$
  5. $\lim\limits_{k\rightarrow\infty}\frac{x_{k+1}-x^*}{x_k-x^*}=\phi'(x)$

• 设$x=\phi(x)$在区间[a,b]有根$x^*$，当$x\in[a,b]$时，$|\phi'(x)|\geq1$，则对任意初始值$x_0\in[a,b]$且$x_0\neq x^*$，迭代公式$x_{k+1}=\phi(x_k)$发散

第3节 牛顿法

$$f(x)=f(x_n)+f'(x_n)(x-x_n)+\frac{f''(x_n)}{2!}(x-x_n)^2+\dots$$

取泰勒公式前两项来替代f(x)，并且当f’(x)不为0时有：

$$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}$$

牛顿法求重根也是收敛的，不过是线性收敛。

第4节 弦线法

设$x_n, x_{n-1}$是$f(x)=0$的两个近似根，它们对应的函数值为$f(x_n), f(x_{n-1})$，过两点做直线，直线方程如下

$p(x) = f(x_n) + \frac{f(x_n)-f(x_{n-1})}{x_n-x_{n-1}}(x-x_n)$

用直线方程替代函数，那么就相当于求解$p(x)=0$的解了

$$x_{n+1} = x_n - \frac{x_n-x_{n-1}}{f(x_n)-f(x_{n-1})}f(x_n)$$

第四章 插值法

第1节 插值定义

设$f(x)$是定义在区间$[a,b]$上的函数，$x_0, x_1,x_2,\dots,x_n$是区间$[a,b]$上n+1个互异的点，若存在一个简单函数$p_n(x)$，满足：

$$p_n(x_i) = f(x_i)=y_i$$

$p_n(x)$是插值函数，求$p_n(x)$的方法称为插值法

第2节 Lagrange插值

2.1 线性插值

两个点$(x_0, y_0), (x_1, y_1)$过两点做直线，所以一次插值也称为线性插值。

$$p_1(x) = y_0 + \frac{y_1-y_0}{x_1-x_0}(x-x_0)$$

2.2 抛物插值

三个点$(x_0, y_0),(x_1, y_1), (x_2, y_2)$过三点做抛物线，所以抛物插值也称为二次插值。

$$p_2(x)= y_0\frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}+ y_1\frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)}+ y_2\frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}$$

2.3 一般情形

$$l_j(x) = \prod\limits_{k=0\\k\neq j}^n \frac{x-x_k}{x_j-x_k}\\ p_n(x) = \sum\limits_{j=0}^n l_i(x)y_i$$

第3节 牛顿插值公式

3.1 差商的概念

$f(x)$关于$x_i, x_j$的一阶差商：记作$f[x_i, x_j] = \frac{f(x_i)-f(x_j)}{x_i-x_j}$，$f(x)$关于$x_i, x_j, x_k$的二阶差商：记作$f[x_i, x_j, x_k] = \frac{f[x_j, x_k]-f[x_i, x_j]}{x_k-x_i}$。一般地，k阶差商为：$f[x_0, x_1,\dots, x_k] = \frac{f[x_1,x_2,\dots,x_k]-f[x_0,x_1,\dots,x_{k-1}]}{x_k-x_0} = \sum\limits_{m=0}^k \frac{f(x_m)}{\prod\limits_{i=0\\i\neq m}^k (x_m-x_i)}$，并且任意改变节点次序，k阶差商值不变。

3.2 牛顿插值

将n次插值多项式写成如下形式：

$$N_n(x) = a_0 + a_1 (x-x_0) + a_2(x-x_0)(x-x_1) + \dots + a_n(x-x_0)(x-x_1)\dots(x-x_{n-1}) = \\ a_0 + \sum\limits_{i=1}^n \left(a_i \prod\limits_{k=0}^i(x-x_k)\right)$$

由插值条件：

$$N_n(x_0) = f(x_0), N_n(x_1) = f(x_1), \dots , N_n(x_n) = f(x_n)$$

可得方程：

$$\left\{ \begin{array}{} a_0 = f(x_0)\\ a_0 + a_1(x_1-x_0) = f(x_1)\\ \dots \dots \\ a_0 + a_1(x_n-x_0)+ \dots + a_n(x_n-x_0)\dots(x_n-x_{n-1}) = f(x_n) \end{array} \right.$$

求解方程：

$$a_0 = f(x_0), a_1 = f[x_0, x_1], a_2 = f[x_0,x_1,x_2],\dots, a_n = f[x_0, x_1, x_2, \dots, x_n]$$

第五章 数值微分

第六章 数值积分