前言
本文是课程作业,Github链接
旅行商问题
旅行商问题(Traveling Salesman Problem, 简称TSP)是一个著名的组合优化问题:在一幅地图上,给定n个城市的坐标,要求从起点出发,经过所有城市再回到起点,路径最短的问题。在数据结构中用图论来描述便是:给定一全连通的无向带权图$G=(V,E)$,需找出总权值最小的Hamilton圈。其中$V={v_1, v_2, v_3,\dots,v_n}$表示n个节点的集合,$E={e_|v_i, v_j \in V}$是集合中节点两两连接的集合,每一条边$e_$都存在与之对应的权值$d_$,其中$d_$为从$i$到$j$的度量,可以是距离、费用、时间、油量等。
旅行商问题描述起来虽然简单,但是解决起来却非常困难。其属于 NP-complete 问题,而且是 NP(non-deterministic poly-nominal)问题中最难的一类问题,如果用穷举法来列出所有解,时间复杂度为$O(n!)$。$n=20\rightarrow 1.2\times 10{18};\quad n=100\rightarrow 4.6\times10{155}$,可以看出,在求解100个节点时候,穷举法基本不可能实现了,毕竟宇宙中的粒子数“仅有”$10^{87}$个。
遗传算法
介绍
遗传算法(Genetic Algorithm, GA)是生命科学与工程科学交叉的产物,其本质是一种求解问题的高度并行的全局随机化搜索算法,有几个基本概念:编码、选择、交叉、变异等。步骤为:选择合适编码、定义种群适应度、确定种群大小、确定最大代数、确定选择方法、确定交叉方法、确定变异方法、定义交叉编译概率等。流程图如下所示:
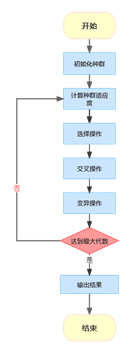
编码方式
在TSP问题中,染色体的编码方式用的是节点编号,为了表示起点城市为编号为0的城市,则第一个染色体编号为0,或者计算适应度时直接加上城市0。
选择方式
使用轮盘赌的方法,即适应度越大的个体越容易被抽到,就好像在一个圆盘上面占的面积最大,这样可以保证选到的概率最大。
$$
i = \frac{costs - costs_i}{costs_-costs_}
$$
上式为适应度计算公式,下面为轮盘赌选择概率公式。
$$
p_i = \frac{\sum\limits_i fitness_i}
$$
交叉方法
这里提供两种方式,方式2可以看成一种优化方法。
- 方法1:选择一个父体,随机生成一个交叉点idx,交换idx前与idx后的序列,注意城市0不要变。
- 方法2:选择一个父体一个母体,随机生成一个交叉点idx,按照母体idx之后的顺序重新排列父体中对应的顺序,按照父体idx之后的顺序重新排列母体中对应的顺序,由下图可以看出。毕竟,有性繁殖比无性繁殖更强大。
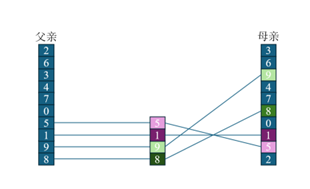
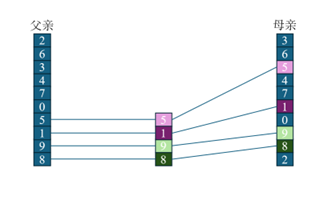
变异
随机选择两个点,交换两点染色体的位置
下一代生成
先对上一代进行适应度评估并按照适应度排序,然后前1/4的个体直接保留到下一代,保留优质基因,下一代1/4的个体经过选择-交叉-变异,下一代1/4的个体经过选择-交叉,下一代1/4的个体经过选择-变异。
代码实现
TSP问题
class TSP:
def __init__(self, node_num, file_path=None, save_path=None):
self.nodes = None
self.node_num = node_num
if not file_path or not os.path.exists(file_path):
self.generate_node_random()
else:
self.load(file_path)
self._generate_distance_table()
if save_path:
self.save(save_path)
# 画图渲染
def render(self,title=None, route: np.ndarray = None, draw_notes=True, draw_route=True, draw_costs=True, draw_node_info=False):
# 画出每个点,然后依次按route画路由,显示costs和rewards,并且不阻塞
plt.cla()
if title:
plt.title(title)
if draw_notes:
# 画除了起点外所有的点
plt.scatter(self.nodes[1:, 0], self.nodes[1:, 1], c='b', s=5)
# 画起点,使用一个五角星,并且大一点
plt.scatter(self.nodes[0, 0], self.nodes[0, 1], c='g', marker='*', s=100)
# 是否标数字与坐标
if draw_node_info:
for i in range(self.node_num):
info = '{:^2d}({:^2d},{:^2d})'.format(i, self.nodes[i, 0], self.nodes[i, 1])
plt.text(self.nodes[i, 0]+0.2, self.nodes[i, 1]+0.2, info, fontsize=8)
if draw_route and route is not None:
# self.nodes 总共包含 self.node_num 个节点,依次连接,并且最后一个节点连接第一个节点
x = np.hstack((self.nodes[route[:self.node_num], 0], self.nodes[route[0], 0]))
y = np.hstack((self.nodes[route[:self.node_num], 1], self.nodes[route[0], 1]))
plt.plot(x, y, c='r')
if draw_costs and route is not None:
plt.text(0, -self.node_num//9, 'costs:{:.4f}'.format(self.evaluate(route)), fontsize=8)
plt.pause(0.1)
# 评估路径,并返回costs
def evaluate(self, route: np.ndarray):
costs = np.sum([self.distance_table[route[i], route[i + 1]] for i in range(self.node_num - 1)])
costs += self.distance_table[route[self.node_num - 1], route[0]]
return costs
def generate_node_random(self): # 随机生成节点
self.nodes = np.vstack((np.array([0, 0]),
np.random.randint([0, 0], [self.node_num, self.node_num],
size=(self.node_num - 1, 2))))
# 生成距离表格
def _generate_distance_table(self):
self.distance_table = np.zeros((self.node_num, self.node_num), dtype=np.float64)
for i in range(self.node_num):
for j in range(i, self.node_num):
self.distance_table[i, j] = TSPGA._get_two_distance_euclidean(self.nodes[i], self.nodes[j])
self.distance_table[j, i] = self.distance_table[i, j]
def load(self, file_path):
if os.path.exists(file_path):
self.nodes = np.load(file_path)
def save(self, file_path):
np.save(file_path, self.nodes)
@staticmethod
def _get_two_distance_euclidean(param, param1): # 计算欧几里得距离
return 0 if param[0] == param1[0] and param[1] == param1[1] else math.sqrt(
(param[0] - param1[0]) ** 2 + (param[1] - param1[1]) ** 2)
GA部分
概览
class GA:
def __init__(self, generation_num, population_num, mutation_rate, crossover_rate, node_num, file_path=None,
save_path=None):
self.idx = None
self.fitness = None
self.costs = None
self.population = None
self.crossover_rate = crossover_rate
self.generation_num = generation_num
self.population_num = population_num
self.mutation_rate = mutation_rate
self.node_num = node_num
self.tsp = TSPGA(node_num, file_path=file_path, save_path=save_path)
# 定义模拟,也就是训练过程
def simulate(self, crossover_num=1, convergence_exit:int=None, separate:bool=False, save_path:str=None, show:bool=False):
pass
# 生成第一代种群
def first_population(self):
pass
# 下一代生成
def next_population(self, parents_num=2, separate=False):
pass
# 选择方法
def select(self, num=2):
pass
# 交叉方法
def crossover(self, parents):
pass
# 变异方法
def mutation(self, child):
pass
# 评估
def evaluate(self):
pass
生成第一代
def first_population(self):
self.population = np.array([np.random.permutation(self.node_num - 1) for _ in range(self.population_num)])
self.population += 1
self.population = np.hstack((np.zeros((self.population_num, 1), dtype=np.int64), self.population))
self.costs = np.zeros(self.population_num, dtype=np.float64)
self.evaluate() # 评估第一代
适应度评估
def evaluate(self):
# 对当前这代进行评估
for i in range(self.population_num):
self.costs[i] = self.tsp.evaluate(self.population[i])
# 对costs归一化
min_val = np.min(self.costs)
max_val = np.max(self.costs)
self.fitness = (max_val - self.costs) * 100 / (max_val - min_val)
self.idx = np.argsort(self.fitness)[::-1]
选择方法
def select(self, num=2):
# 按照costs从小到大排序,获取下标,然后按照概率选择
return np.random.choice(np.arange(self.population_num), num, replace=False,
p=self.fitness / np.sum(self.fitness))
交叉方法
def crossover(self, parents):
# 判断是一个父母还是两个父母
if len(parents) == 1:
# 父母只有一个,就是把它自己前后交叉
# 选择交叉点
# 交叉点不能是0和node_num-1
# 交换 1:交叉点-1 与 交叉点:node_num-1 -> 0, idx:end, 1:idx-1
idx = np.random.randint(2, self.node_num - 1)
child = np.hstack((self.population[parents[0]][0:1], self.population[parents[0]][idx:],
self.population[parents[0]][1:idx]))
return child
elif len(parents) == 2:
# parents[0]为母亲,parents[1]为父亲
# 在父亲中选出交叉点idx,选择父亲中idx之后的点
# 然后在母亲中寻找到父亲idx之后的所有点,按照父亲中idx之后的点的顺序,重新排列
idx = np.random.randint(2, self.node_num - 1) # 选择交叉点
mother = self.population[parents[0]].copy()
father = self.population[parents[1]].copy()
mother_X = mother[idx:].copy() # 母亲交叉点之后的染色体
father_X = father[idx:].copy() # 父亲交叉点之后的染色体
# 找出父亲染色体在母亲中的位置
mother_idxs = np.array([np.where(mother == i)[0][0] for i in father_X])
# 找出母亲染色体在父亲中的位置
father_idxs = np.array([np.where(father == i)[0][0] for i in mother_X])
# 对位置进行排序
mother_idxs.sort()
father_idxs.sort()
# 按照母亲的位置,重新排列父亲的染色体
mother[mother_idxs] = father_X
father[father_idxs] = mother_X
return np.vstack((mother, father))
变异方法
def mutation(self, child):
# 随机选择两个不同的点,进行交换
# 不同点不能是0
idx1, idx2 = np.random.choice(np.arange(1, self.node_num), 2, replace=False)
child[idx1], child[idx2] = child[idx2], child[idx1]
return child
下一代生成
def next_population(self, parents_num=2, separate=False):
"""
生成下一代
:param separate:是否优化下一代生成算法,True表示优化下一代生成算法,即(上代优解,交叉且变异,交叉不变异,变异不交叉)
:param parents_num: 是否优化交叉方案,如果为1,表示只有一个父母,表示不优化交叉方案;如果为2,表示有两个父母,表示优化交叉方案
:return:
"""
next_population = np.zeros(shape=(self.population.shape[0], self.population.shape[1]), dtype=np.int64)
i = 0
s = self.population_num//4 if separate else self.population_num
while i < s:
# 选择
parents = self.select(num=parents_num)
# 交叉
if np.random.rand() < self.crossover_rate: # 需要交叉
next_population[i:i + parents_num] = self.crossover(parents)
else: # 不需要交叉
next_population[i:i + parents_num] = self.population[parents].copy()
# 变异
for j in range(parents_num):
if np.random.rand() < self.mutation_rate:
next_population[i+j] = self.mutation(next_population[i+j])
i += parents_num
if separate:
# 只交叉,不变异
while i < self.population_num*2//4:
# 选择
parents = self.select(num=parents_num)
# 交叉
if np.random.rand() < self.crossover_rate: # 需要交叉
next_population[i:i + parents_num] = self.crossover(parents)
else: # 不需要交叉
next_population[i:i + parents_num] = self.population[parents].copy()
i += parents_num
# 只变异,不交叉
while i < self.population_num*3//4:
# 选择
parents = self.select(num=1)
# 变异
next_population[i] = self.mutation(self.population[parents[0]].copy())
i += 1
next_population[i:] = self.population[self.idx[:len(next_population)-i]].copy()
self.population = next_population
self.evaluate() # 评估这一代
训练过程
def simulate(self, crossover_num=1, convergence_exit:int=None, separate:bool=False, save_path:str=None, show:bool=False):
"""
遗传算法仿真全过程
:param crossover_num: 是否优化交叉方案,如果为1,表示只有一个父母,表示不优化交叉方案;如果为2,表示有两个父母,表示优化交叉方案
:param convergence_exit: 收敛后是否自动退出,如果为None,表示不自动退出,如果为int表示,退出的计数次数
:param separate: 是否优化下一代生成算法,True表示优化下一代生成算法,即(上代优解,交叉且变异,交叉不变异,变异不交叉)
:param save_path: 结果保存路径,保存每一代的结果
:param show: 是否可视化显示
:return:
"""
self.first_population()
# 保存每一代的最优结果
rst = np.zeros(shape=(self.generation_num, self.node_num), dtype=np.int64)
rst[0] = self.population[self.idx[0]]
last_costs = self.costs[self.idx[0]]
if convergence_exit is not None:
count = convergence_exit
else:
count = 0
for i in range(self.generation_num-1):
print(f'第{i+1}代{self.population.shape[0]}个个体最优成本为{self.costs[self.idx[0]]}')
self.next_population(parents_num=crossover_num, separate=separate)
rst[i+1] = self.population[self.idx[0]]
if show:
self.tsp.render(route=self.population[self.idx[0]])
if convergence_exit is not None:
if abs(last_costs - self.costs[self.idx[0]]) < 1e-12:
count -= 1
if count == 0:
break
else:
count = convergence_exit
last_costs = self.costs[self.idx[0]]
print(f'最终代第{self.generation_num}代{self.population.shape[0]}个个体最优成本为{self.costs[self.idx[0]]}')
if save_path:
if os.path.exists(save_path):
data = np.load(save_path)
node_num_of_data = data.shape[1]
if node_num_of_data == self.node_num:
my_best_costs = self.tsp.evaluate(self.population[self.idx[0]])
data_best_costs = self.tsp.evaluate(data[-1])
print(f'当前最优成本为{my_best_costs},数据中最优成本为{data_best_costs}', end=', ')
if my_best_costs < data_best_costs:
print('保存当前结果')
np.save(save_path, rst)
else:
print('不保存当前结果')
else:
print('无存在的文件,直接保存当前结果')
np.save(save_path, rst)
