数据结构--图

1、基本概念

极大连通、极小连通、极大连通子图、极小连通子图、连通分量

无向图

• 极大连通

  在无向图中，指的是任意两点都有直接或者间接的路径

• 极小连通

  在无向图中，生成树就是一个极小连通；如果加一条边就会形成一个环，如果减一条边就会出现孤立的节点；n个节点应该有n-1条边

• 极大连通子图和极小连通子图

  满足上述极大连通和极小连通的子图

• 连通分量

  指的是极大连通子图的数目

• 思考：假如一个图有n个节点

  如果边数小于n-1的话，此图必定是非连通图

  非连通图最多应该有 $\frac{(n-1)(n-2)}{2}$ 条边 ，解释：由n-1构成完全图，如果此时再加入一条边，那么就会形成连通图了

强连通图、强连通分量、弧

有向图

• 弧

  弧头：有箭头的那一端

  弧尾：无箭头的那一端

• 强连通图

  有向图中，任意两个顶点都有直接或者间接的路径到达（注意，路径是有方向的），此图称为强连通图

• 强连通分量

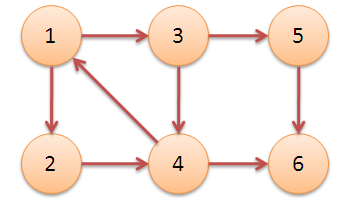
  有向图的强连通子图的数量就是强连通分量，书上是说‘有向图的极大连通子图就是强连通分量’

  如下图所示，三个强连通分量 {1,2,3,4}, {5},

  

• 思考：假如有n个节点的有向图

  强连通情况下，至少需要n条边；解释：构成一个环就行了，这样，任意两点直接都可循环到达。

生成树与最小生成树

• 生成树

  无向图$G = (V,E)$和无向图图$G^1 = (V^1, E^1)$，若$G^1包含G$的所有顶点，且边是$G$的子集，那么$G^1就是G的生成树$

  生成树不唯一

  维基百科如下图定义

  

• 最小生成树

  每条边都有权值，最小生成树就是最后生成的树，权值和最小

2、图的存储

邻阶矩阵

• 有向图：节点i到节点j有权重为m的边，那么零阶矩阵中$a_{ij} = m$
• 无向图：节点i到节点j有权重为m的边，那么零阶矩阵中$a_{ij} = a_{ji} = m$
• 零阶矩阵中出现为0或者∞的情况就是，对应于不带权图与带权图中没有边

邻阶表

设有n个节点，则存在长度为n的指针数组（下标从1开始）

下标为i的指针指向了一个链表，这个链表依次是节点i指向的节点（有向图）或者节点i连接的节点（无向图）。

十字链表（有向图）

• 弧节点：tailvex, headvex, hlink, tlink, info

  tailvex: 指向弧尾的节点的指针

  headvex: 指向弧头的节点的指针

  hlink：指向弧头相同的下一条弧节点

  tlink：指向弧尾相同的下一条弧节点

  info：指向弧的信息

• 顶点节点：data, firstin, firstout

  data：存放数据信息

  firstin：指向第一个以该节点为弧头的弧节点

  firsstout：指向第一个以该节点为弧尾的弧节点

领接多重表（无向图）

• 边节点：mark, ivex, ilink, jvex, jlink, info

  mark: 标志域，表示该条边是否被搜索过

  ivex，jvex：指向该边依附的两个顶点

  ilink，jlink：指向下一条依附ivex，jvex的边

  info：指向信息域

• 顶点节点: data, firstedge

  data：该节点的信息

  firstedge：指向第一条依附于该节点的边

3、广度搜索和深度搜索

深度优先搜索与深度搜索树/森林

时间复杂度

• 领接表：$O(|V|+|E|)$
• 领接矩阵：$O(|V|^2)$

空间复杂度

$O(|V|)$

广度优先搜索与广度优先搜索树/森林

时间复杂度

• 领接表：$O(|V|+|E|)$
• 领接矩阵：$O(|V|^2)$

空间复杂度

$O(|V|)$

4、最小生成树算法（无向图）

Prim算法

时间复杂度：$O(|V|^2)$只跟节点数有关，与边无关。

我原称之为：大孤岛算法，也就是所有的节点是孤岛，然后依次把每个节点加入到大孤岛中来。

步骤：

• 1、从节点$V_n$开始，加入到该 “大孤岛” 中
• 2、寻找 “大孤岛” 相连 最小权值 的边，该边连接的节点加入 “大孤岛” 中
• 3、重复2，直到所有的节点都加入了 “大孤岛” 中

Kruskal算法

时间复杂度：$O(|E|log|E|)$只跟边数有关，与节点数无关。

我原称之为：多孤岛算法，也就是把所有的节点看作一个孤岛，然后依次寻找两个孤岛之间最小的边，将两个孤岛连接成一个孤岛

可以使用并查集

步骤：

• 1、找到一条最小权值的边，该条边满足连接着两个 “孤岛” ，不是两个节点哦
• 2、将上述两个孤岛变成一个孤岛
• 3、重复1、2两步

5、最短路径算法

Dijkstra算法

时间复杂度：$O(|V|^2)$，只跟节点数有关

不适用于有负权边

求解单源路径最短问题（即，节点$V_0$到所有节点的最短路径）

步骤：

• 参数介绍：

  • flag数组：标志当前节点是否找到了最短的路径

  • dist数组：长度

  • path数组：上一个节点

  • 初始化：flag全都是false，path全都是-1，dist全都是无穷大

• 从$V_n$出发，找到$V_n$的所有出边，将权值加$V_n$的dist填入dist数组，path数组都填$V_n$

• 然后从dist数组中找到最小的一条边且flag为false，下标就是下一个节点$V_m$

• 从上一步来的，$V_m$的flag变成true，然后找到$V_m$所有出边，依次更新出边的节点，如果发现从$V_m$会更加小，那么就更新path和dist

  • 重复第2、3步，直到flag全都是true

Floyd算法

时间复杂度：$O(|V|^3)$，只跟节点数有关

适用于有负权边，但不适用于有负权回路边

求解两两节点之间最短路径

步骤：

• 参数介绍：

  A矩阵：$a_{ij} =$从节点i到j的最短路径

  path矩阵：$p_{ij} =$从节点i到节点j的中转节点

  初始化：A矩阵为邻阶矩阵，path矩阵为-1

• 从$V_0$出发，依次求解到$V_1,V_2,...,V_{n}$的最短路径

  如求$V_0 \rightarrow V_1$的最短路径

  • 依次找以$V_2,V_{n}$作为中转节点，路径是否更小，更小就更新A和path矩阵

• 重复上述步骤

6、拓扑排序与关键路径（AOV与AOE）

AOV（有向无权图），拓扑排序

顶点：事件；边：无关紧要；

时间复杂度：

• 领接表：$O(|V|+|E|)$
• 零阶矩阵：$O(|V|^2)$

方法1、步骤：（正拓扑序）

• 找入度为0的节点，写入排序数组
• 删除上面所找的节点以及连接他们的出边
• 重复上述两步，直到图空了；如果第一步已经找不到了，但是图不空，说明有回路，拓扑排序失败

方法2、步骤：（逆拓扑序）

• 找出度为0的节点，写入排序数组
• 删除上面所找的节点以及连接他们的入边
• 重复上述两步，直到图空了；如果第一步找不到，但是图不空，说明有回路，拓扑排序失败。

AOE（有向带权图），关键路径

顶点：事件；边：活动

需要能够拓扑排序

时间复杂度：因为是利用拓扑排序来求的，所以跟拓扑排序一样，没有验证

步骤：

• 直接找起点到重点最长的路径，可能有多条

• 参数介绍：

  • ve数组、vl数组：事件（节点）最早、最晚发生时间
  • e数组、l数组：活动（边）最早、最晚发生时间
  • l-e数组：l数组减去e数组，为0表示这个是关键路径上的一条边
  • ve、vl数组长度与节点数一样，然后初始化为0即可
  • e、l、l-e数组长度与边数一样，初始化为0即可

• 处理ve数组

  • 从起点开始：起点对应的值为0
  • 依次找起点的出边，然后出边对应的节点为$V_m$，并且出边的弧头的ve值为起点的ve值加边权值
  • $V_m$的ve值是：$V_m$所有的入边弧头ve的 最大值 ，然后依次找$V_m$的出边，出边弧头对应的ve是$V_m$的ve加边权值
  • 重复上面步骤

• 处理vl数组

  • 从终点开始：终点对应的vl值是终点的ve值
  • 依次找终点的入边，然后入边对应的节点为$V_m$，并且入边的弧尾的vl值尾起点的vl值减去边权值
  • $V_m$的vl值是：$V_m$所有的出边弧尾ve的 最小值 ，然后依次找$V_m$的入边，入边弧尾对应的ve是$V_m$的ve减去边权值
  • 重复上面步骤

• 处理e数组：为弧尾对应的ve值

• 处理l数组：为弧头对应的vl值减去该弧的权值

• 处理l-e数组：l数组减去e数组即可

如何加快整体工程的进度：

• 加快所有关键路径的进度

7、Graphviz简单介绍

​ Graphviz是用来可视化图和树的工具，常用.dot文件或者api进行操作，官网链接。

用法一、dot文件使用

目前还不会使用这个软件，先挖坑。